GB = GG + GLi = mG * g +
mLi * g
Aus der Dichte pLi, der Luft im Inneren des Ballons Und dem
Volumen V des aufgeblasenen Ballons erhält man für die Gewichtskraft
der Luft:
GLi = mLi * g = pLi * VB * g
F= GB -FA -FL
=mG * g + pLi * VB * g - pLa * VB *g-FL
=mG * g+(pLi -pLa)*VB * g-FL
Den Term mG * g + (pLi - pLa) * VB *
g kann man als effektive Gewichtskraft des Ballons interpretieren. Da
pLi größer als pLa ist, ist die effektive
Gewichtskraft eines aufgeblasenen Luftballons größer als die eines
leeren. Auf diesen wirkt nämlich nur die Gewichtskraft des Gummis, die
Gewichtskraft der Luft im Inneren des Ballons entfällt, die Auftriebskraft
kann gegenüber der Gewichtskraft vernachlässigt werden. Da bei einem
leeren Ballon und den hier betrachteten kurzen Fallstrecken auch der
Luftwiderstand gegenüber der Gewichtskraft des Gummis vernachlässigt
werden kann, wirkt auf ihn in guter Näherung als einzige Kraft die
Gewichtskraft des Gummis, Der leere Ballon führt also eine Bewegung mit
konstanter Beschleunigung durch.
Anders ist die Situation beim aufgeblasenen Luftballon. Hier spielt der mit der
Geschwindigkeit zunehmende Luftwiderstand eine entscheidende Rolle, so dass
trotz der höheren Gewichtskraft bereits nach kurzer Fallstrecke
FL = mG * g + (pLi - pLa) * VB * g
gilt, und die Bewegung mit konstanter Geschwindigkeit erfolgt.
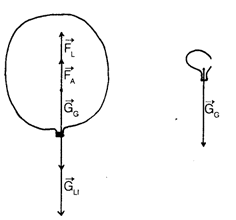
Bild 4 Fall eines aufgeblasenen und eines leeren Luftballons.
GG: Gewichtskraft des Gummis; GLi Gewichtskraft der Luft im Inneren des Ballons; FA: Auftriebskraft, FL: Luftwiderstand. Die Länge der Kraftpfeile wurde nicht maßstabgetreu gezeichnet.