1. Punkt - Ebene
2. Punkt - Gerade (V1)
3. Windschiefe Geraden
4. Punkt - Gerade (V2)
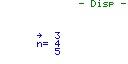
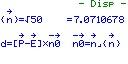
1. Punkt - Ebene
Nach jeder Eingabe des Zahlenwertes wird
verlangt, um diese zu bestätigen.Zuerst ist die Eingabe der Normalform der Ebene erforderlich
E: ax+by+cz=f
Man nehme an sie lautet 3x+4y+5z=1
So wird jede Zahl für jeden Parameter seperat eingegeben und dann bestätigt.
a = 3 b = 4 c = 5 f = 1
Dann wird nach dem Punkt in der Ebene gefragt.
Nehmen wir an er sei P(100 | 200 | 300)
Wie eben, auch hier alles mit
bestätigen.Nun wird nach dem Punkt gefragt.
Nehmen wir an er ist im Ursprung, also (0 | 0 | 0)
Nach kompletter Eingabe wird als erstes der Normalenvektor ausgegeben
Nach weiterer Bestätigung wird die Länge von diesem angezeigt. (sqrt = Wurzel)
Also sqrt(50) = 7,0710678
Nach erneuten
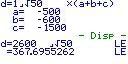
Druck wird nochmal eine Zusammenfassung dargestellt, in der auch gezeigt wird wie man darauf kommt.Zudem wird d angezeigt, was dem Abstand entspricht. Sowohl als gemeiner Bruch als auch Dezimalbruch, mit entsprechender Einheit.
LE = Längeneinheiten.
Achtung!
Man sollte darauf achten, dass der Normalenvektor nicht die Länge 0 als Ergebnis hat. Sonst hat es zur Folge, dass der Rechner durch 0 dividiert und somit kein Ergebnis bringt.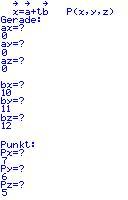
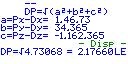
2. Punkt - Gerade (V1)
Im ersten Schritt dieser Berechnung wird nach der Geraden gefragt, in Vektorform.
Nehmen wir für unseren Stützvektor der Geraden die Punkte x = 0, y = 0, z = 0, also den Koordinatenursprung.
So wird für ax = 0, bx = 0 und zx = 0 eingegeben.
Nun wird nach Richtungsvektor gefragt.
Nehmen wir an er sei bei (10 | 11 | 12).
So geben wir für bx = 10 by = 11 und für bz = 42 ein.
Jetzt fragt das Programm nach dem Punkt.
Dieser ist im Beispiel bei (7 | 6 | 5).
So geben wir bei Px = 7, Py = 6 und Pz = 5 ein.
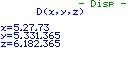
Im nachfolgenden Fenster wird nach dem - Disp - xd, yd und zd gezeigt und wie es errechnet wird.
Im nächsten Fenster nach einer weiteren Betätigung von
wird D mit den jeweiligen Punkten angezeigt. Im letzten Bild zeigt der Rechner an wie der Abstand berechnet wird.
Der Abstand wird dann in der letzten Zeile angezeigt mit DP als Dezimal in LE (Längeneinheiten)
Achtung!
Man sollte darauf achten, dass der Punkt nicht auf der Geraden liegt. Sonst hat es zu Folge, dass der Abstand 0 beträgt..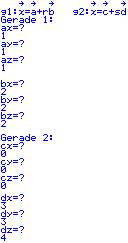
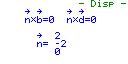
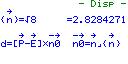
3. Windschiefe Geraden
Wie immer jede Eingabe mit
bestätigen, auch um zu den Ergebnisbildern zu kommen.In diesem Programm werden die Vektoren eingegeben.
Für unser Beispiel.
Für den Stützvektor der ersten Gerade: (1 | 1 | 1).
Für den Richtungsvektor (2 | 2 | 2).
Nun folgt der Stützvektor der zweiten Gerade: (0 | 0 | 0).
Für den Richtungsvektor dieser (3 | 3 | 4).
Das erste Fenster zeigt den Normalenvektor.
Das zweite Fenster ziegt das Ergebnis den Betrag Normalenvektors.
Nun wird der Rechenweg für d, also dem Abstand angezeigt und im Nachfolgenden das Ergebnis.
In der Bruchschreibweise und im Dezimalzahl mit entsprechender Einheit
LE (Längeneinheiten)
In diesem Fall haben die zwei Geraden keinen Abstand, sondern schneiden sich im Ursprung.
Achtung!
Man sollte darauf achten, dass die Richtungsvektoren nicht gleich sind, denn sonst wären es Parallelen.Der Normalenvektor sollte auch nicht 0 betragen sonst kommt es zu keinem Ergebnis.
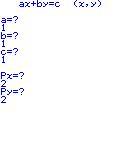
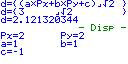
4. Punkt - Gerade (V2)
Der Rechner fragt in diesem Programmmenü ab, welche Parameter die Gerade hat. Es steht da: ax+by=c
Für die Gerade müssen a, b und c eingegeben werden.
a = 1, b = 1 und c = 1
Da sich alles in einer Ebene abspielt, reichen die x und y Koordinaten.
Px ist in dem Fall unsere x-Koordinate und Py unsere y-Koordinaate des Punktes. (2 | 2)
Nach erfolgreicher Eingabe zeigt der Rechner den Normalenvektor und die Hessische Normalenform an.
Nach erneuten Tastendruck, wird im Display der Abstand angezeigt, in diesem Fall ist es d. Nach - Disp - steht nochmal die Eingabe.