Das Listen-Menü
Auswählen und Erstellen einer Listendatei
Listen-Summe, -Min, -Max
Listen-Durchschnitt
arithmetische Mittel einer Liste
Listeninhalte in Prozent
Anwendungen
Aufgaben
Grundlagen
Mit Listen kann genau so gerechnet werden, wie mit Variablen. Sie
können im Run-, Mat-, Graph-, Table-Menü verwendet werden.
Generell kann eine Liste über 
 (List)
(List)
 (List) (1-6)
(List) (1-6)
 aufgerufen werden. Werden wie im folgenden Bild zwei komplette Listen
miteinander multipliziert, so wird Zelle 1 der 1. Liste mit Zelle 1 der
2. Liste, Zelle 2 der 1. Liste mit Zelle 2 der 2. Liste usw.
multipliziert.
aufgerufen werden. Werden wie im folgenden Bild zwei komplette Listen
miteinander multipliziert, so wird Zelle 1 der 1. Liste mit Zelle 1 der
2. Liste, Zelle 2 der 1. Liste mit Zelle 2 der 2. Liste usw.
multipliziert.

Soll jedoch mit einer ganz bestimmten Zelle gerechnet werden, so wird
die Zellennummer in eckigen Klammern hinter die Liste geschrieben.

Zurück
Auswählen der Listendatei
Es gibt insgesamt 6 Dateien zu je 6 Listen. Zwischen diesen kann man
wechseln, wenn im List-Menü das Setup-Menü über 
 aufgerufen wird. In der ersten Zeile kann nun über
aufgerufen wird. In der ersten Zeile kann nun über
 bis
bis
 Datei 1 - 6 gewählt werden.
Datei 1 - 6 gewählt werden.
Erstellen einer Liste
Es gibt mehrere Möglichkeiten eine Liste zu erstellen.
Variante 1: Listenwerte einzeln im List-Menü eingeben
Dazu wird im List-Menü mit dem Curser die betreffende Liste
gewählt und dann die Werte beginnend mit der ersten Reihe
eingegeben.
Variante 2: Spalte einer Matrix in eine Liste kopieren
(Voraussetzung: Es muss eine Matrix mit Werten vorhanden sein)
Dazu wird im Run-Menü folgende Befehlszeile eingegeben: 
 (MAT)
(MAT)
 (M->L)
(M->L)

 (Matrix A)
(Matrix A)

 (Spalte 1 der Matrix)
(Spalte 1 der Matrix)



 (LIST)
(LIST)
 (List) Nun noch die Listennummer eingeben, wohin die Matrixspalte kopiert werden soll.
(List) Nun noch die Listennummer eingeben, wohin die Matrixspalte kopiert werden soll.


Variante 3: Spalte einer Tabelle in eine Liste kopieren
(Voraussetzung: Es muss eine Tabelle mit Werten vorhanden sein)
Das Table-Menü wird aufgerufen. Mit
 werden je nachdem wieviele Funktionen gewählt sind eine oder
mehrere Tabellen generiert. Nun kann mit dem Curser die Spalte
ausgewählt werden, die in eine Liste kopiert werden soll. Mit
folgender Befehlszeile wird dies nun ausgeführt:
werden je nachdem wieviele Funktionen gewählt sind eine oder
mehrere Tabellen generiert. Nun kann mit dem Curser die Spalte
ausgewählt werden, die in eine Liste kopiert werden soll. Mit
folgender Befehlszeile wird dies nun ausgeführt: 
 (LIST)
(LIST)
 (LMEM) Je nachdem, auf welche Liste die Spalte kopiert werden soll
(LMEM) Je nachdem, auf welche Liste die Spalte kopiert werden soll
 bis
bis

Zurück
Im Folgenden werden Operationen erklärt, mit denen man mit Listen
rechnen kann. Der Ablauf funktioniert im Rum-Menü genau so, wie im
List-Menü. Im List-Menü muss aber noch mit dem Curser ein
freies Feld gewählt werden, in das das Ergebnis ausgegeben wird.
Berechnen der Summe einer Liste
Es wird die Summe der Liste 1 errechnet:

 (List)
(List)


 (Sum)
(Sum)

 (List)
(List)


Berechnen des Minimums in einer Liste
Es wird das Minimum in der Liste 1 berechnet:

 (List)
(List)

 (Min)
(Min)


 (List)
(List)



Berechnen des Maximums in einer Liste
Es wird das Maximum in der Liste 1 berechnet:

 (List)
(List)

 (Max)
(Max)


 (List)
(List)



Zurück
Berechnen des arithmetischen Mittels einer Liste
Es wird der Durchschnitt aller Werte von Liste 1 berechnet:

 (List)
(List)

 (Mean)
(Mean)


 (List)
(List)



Zurück
Berechnen des Produktes aller Werte einer Liste
Berechnung des Produktes aller Werte der Liste 1:

 (List)
(List)


 (Prod)
(Prod)

 (List)
(List)


Zurück
Umrechnen der Werte einer Liste in die prozentualen Anteile an der Summe der Liste
Umrechnen der Werte in der Liste 1:

 (List)
(List)


 (%)
(%)

 (List)
(List)


Zurück
Anwendungen in der Physik
- Es ist eine Wertetabelle mit Weg und Zeit einer beschleunigten
Bewegung gegeben. Mit Hilfe des List-Menüs soll herausgefunden
werden, ob es sich um eine gleichmäßig beschleunigte
Bewegung handelt, oder nicht.
| Weg in km |
0,001 |
0,004 |
0,009 |
0,016 |
0,025 |
0,036 |
| Zeit in s |
1 |
2 |
3 |
4 |
5 |
6 |
Um diese Aufgabe zu lösen, ruft man das List-Menü auf. In
Liste 1 wird die Zeit eingetragen und in Liste 2 der Weg. Wenn sich
noch Werte in einder dieser Listen befinden, werden diese
gelöscht. Dazu geht man mit dem Curser in die betreffende Liste
und wählt über  (DEL-A) alles
löschen. Nun geht man mit dem Curser in die Liste 1 und gibt die
Zeit ein. Ebenso wird der Weg in Liste 2 eingetragen.
(DEL-A) alles
löschen. Nun geht man mit dem Curser in die Liste 1 und gibt die
Zeit ein. Ebenso wird der Weg in Liste 2 eingetragen.

Mit der Formel 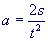 kann die Beschleunigung berechnet werden. Davor muss aber der Weg noch
von km in m umgerechnet werden. Mit dem Curser wird Liste 2
gewählt. (Listenkopf ist dunkel hinterlegt) Nun wird folgendes
eingegeben:
kann die Beschleunigung berechnet werden. Davor muss aber der Weg noch
von km in m umgerechnet werden. Mit dem Curser wird Liste 2
gewählt. (Listenkopf ist dunkel hinterlegt) Nun wird folgendes
eingegeben:

 (LIST)
(LIST)
 (List)
(List)






Mit  noch bestätigen:
noch bestätigen:
Jetzt kann aus diesen Werten die Beschleunigung berechnet werden. Diese
soll in Liste 3 gespeichert werden. Es wird Liste 3 mit dem Curser
gewählt und folgendes eingegeben:


 (LIST)
(LIST)
 (List)
(List)

 (List)
(List)


Mit  wird nun noch bestätigt:
wird nun noch bestätigt:
In jeder Zeile beträgt die Beschleunigung 2 ms-2, dass bedeutet, es handelt sich um eine gleichmäßig beschleunigte Bewegung.
- Eine Wertetabelle mit Frequenzen ist gegeben. Diese sollen in
die dazugehörigen Wellenlängen umgerechntet werden. Die
Formel dazu lautet:
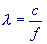
| Lichtfarbe |
violett |
blau |
grünblau |
grün |
gelb |
orange |
rot |
| Frequenz f in 1014 Hz |
7,4 |
6,5 |
6,1 |
5,5 |
5,1 |
4,9 |
4,0 |
Um diese Aufgabe zu lösen, ruft man zuerst das List-Menü auf.
Liste 1 soll dabei die Frequenzen enthalten und Liste 2 die
Wellenlängen. Wenn sich noch Werte in einder dieser Listen
befinden, werden diese gelöscht. Dazu geht man mit dem Curser in
die betreffende Liste und wählt über  (DEL-A) alles löschen. Nun geht man mit dem Curser in die erste Zeile der Liste 1 und gibt die Frequenzen einzeln ein.
(DEL-A) alles löschen. Nun geht man mit dem Curser in die erste Zeile der Liste 1 und gibt die Frequenzen einzeln ein.

Nun wird die Wellenlänge berechnet. Dazu muss mit dem Curser im
Listenkopf Liste 2 gewält werden und dann die Formel zur
Berechnung eingegeben werden: 







 (LIST)
(LIST)
 (List)
(List)


Nun noch mit
 bestätigen.
bestätigen.
Die genauen Werte können abgelesen werden, indem man mit den Curser in der Liste den betreffenden Wert wählt.
Zurück
Aufgaben
1. Schweredruck in einer Wassersäule
(Ph E-Phase)
Eine quadratische Wassersäule mit einer Kantenlänge von 80 cm ist gegeben. Zu berechnen sind V in m3, m in kg, Fg in N und p in Pa für die Höhen 1 m, 2 m, 10 m, 20 m, 50 m und 100 m.
Lösung
Zurück
2. Federkonstantenberechnug
(Ph-LK 11/I)
Die Dehnung einer Feder s wurde in Abhängigkeit der
angehängten Masse m gemessen. Berechnen Sie die auf die Feder
wirkende Kraft F und die Federkonstante D mit Hilfe des
List-Menüs. Geben Sie F als Funktion von s an (Stat-Menü) und stellen Sie die Funktion graphisch (Graph-Menü) dar.
| m in g |
50 |
100 |
150 |
200 |
250 |
300 |
| s in cm |
1,9 |
3,8 |
5,2 |
7,8 |
9,7 |
11,7 |
Lösung
Zurück
3. Berechnungen am Kondensator
(Ph-LK 11/II)
Ein Frequenzgenerator liefert eine Wechselspannung mit dem Effektivwert Ueff=2,2
V und variabler Frequenz. Er wird mit einem Kondensator verbunden. Bei
verschiedenen Frequenzen f werden folgende Werte der
Effektivstromstärke Ieff gemessen:
| f in Hz |
500 |
1000 |
1500 |
2000 |
2500 |
3000 |
| Ieff in mA |
0,112 |
0,224 |
0,336 |
0,448 |
0,560 |
0,672 |
- Berechnen Sie für die gegebenen Frequenzen jeweils den kapazitiven Wiederstand Xc
Zeichnen Sie das f-Xc-Diagramm.
- Zeigen Sie, dass der kapazitive Wiederstand Xc umgekehrt proportional zur Frequenz f ist, indem Sie für alle Messwerte das Produkt Xc·f berechnen. Geben Sie Xc als Funktion von f an.
- Berechnen Sie die Kapazität des Kondensators
Lösung
Zurück


 (List)
(List)
 (List) (1-6)
(List) (1-6)
 aufgerufen werden. Werden wie im folgenden Bild zwei komplette Listen
miteinander multipliziert, so wird Zelle 1 der 1. Liste mit Zelle 1 der
2. Liste, Zelle 2 der 1. Liste mit Zelle 2 der 2. Liste usw.
multipliziert.
aufgerufen werden. Werden wie im folgenden Bild zwei komplette Listen
miteinander multipliziert, so wird Zelle 1 der 1. Liste mit Zelle 1 der
2. Liste, Zelle 2 der 1. Liste mit Zelle 2 der 2. Liste usw.
multipliziert. 


 aufgerufen wird. In der ersten Zeile kann nun über
aufgerufen wird. In der ersten Zeile kann nun über
 bis
bis
 Datei 1 - 6 gewählt werden.
Datei 1 - 6 gewählt werden.



 (MAT)
(MAT)
 (M->L)
(M->L)

 (Matrix A)
(Matrix A)

 (Spalte 1 der Matrix)
(Spalte 1 der Matrix)



 (LIST)
(LIST)
 (List) Nun noch die Listennummer eingeben, wohin die Matrixspalte kopiert werden soll.
(List) Nun noch die Listennummer eingeben, wohin die Matrixspalte kopiert werden soll.


 werden je nachdem wieviele Funktionen gewählt sind eine oder
mehrere Tabellen generiert. Nun kann mit dem Curser die Spalte
ausgewählt werden, die in eine Liste kopiert werden soll. Mit
folgender Befehlszeile wird dies nun ausgeführt:
werden je nachdem wieviele Funktionen gewählt sind eine oder
mehrere Tabellen generiert. Nun kann mit dem Curser die Spalte
ausgewählt werden, die in eine Liste kopiert werden soll. Mit
folgender Befehlszeile wird dies nun ausgeführt: 
 (LIST)
(LIST)
 (LMEM) Je nachdem, auf welche Liste die Spalte kopiert werden soll
(LMEM) Je nachdem, auf welche Liste die Spalte kopiert werden soll
 bis
bis



 (List)
(List)


 (Sum)
(Sum)

 (List)
(List)




 (List)
(List)

 (Min)
(Min)


 (List)
(List)




 (List)
(List)

 (Max)
(Max)


 (List)
(List)




 (List)
(List)

 (Mean)
(Mean)


 (List)
(List)




 (List)
(List)


 (Prod)
(Prod)

 (List)
(List)




 (List)
(List)


 (%)
(%)

 (List)
(List)



 (DEL-A) alles
löschen. Nun geht man mit dem Curser in die Liste 1 und gibt die
Zeit ein. Ebenso wird der Weg in Liste 2 eingetragen.
(DEL-A) alles
löschen. Nun geht man mit dem Curser in die Liste 1 und gibt die
Zeit ein. Ebenso wird der Weg in Liste 2 eingetragen. 
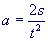 kann die Beschleunigung berechnet werden. Davor muss aber der Weg noch
von km in m umgerechnet werden. Mit dem Curser wird Liste 2
gewählt. (Listenkopf ist dunkel hinterlegt) Nun wird folgendes
eingegeben:
kann die Beschleunigung berechnet werden. Davor muss aber der Weg noch
von km in m umgerechnet werden. Mit dem Curser wird Liste 2
gewählt. (Listenkopf ist dunkel hinterlegt) Nun wird folgendes
eingegeben:
 (LIST)
(LIST)
 (List)
(List)







 noch bestätigen:
noch bestätigen:



 (LIST)
(LIST)
 (List)
(List)


 (List)
(List)



 wird nun noch bestätigt:
wird nun noch bestätigt:

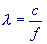
 (DEL-A) alles löschen. Nun geht man mit dem Curser in die erste Zeile der Liste 1 und gibt die Frequenzen einzeln ein.
(DEL-A) alles löschen. Nun geht man mit dem Curser in die erste Zeile der Liste 1 und gibt die Frequenzen einzeln ein.









 (LIST)
(LIST)
 (List)
(List)


 bestätigen.
bestätigen.

