Einführung 5: Differentialrechnungmit dem GTR
5.1 Erläuterungen:
Differentialquotient
Extrema
Wendepunkte
5.2 Differentialrechnung im Graph-Menü:
Anzeigen des Differentialquotienten mit Trace
Anzeigen von Tangenten und Normalen
Ermitteln der Extrempunkte
5.3 Differentialrechnung im Run-Menü
5.4 Differentialrechnung im Table-Menü
Die hier gemachten Ausführungen sollen eine Hilfe für das Lösen von Aufgaben aus dem Themengebiet der Differentialrechnung mit dem GTR sein. Die Erläuterungen beziehen sich auf einige hierfür notwendige Begriffe. Sie sind nicht vollständig und dem besseren Verständniss wegen vereinfacht. D.h. es wird zum Beispiel nichts über Bedingungen bzw. Voraussetzungen gesagt. ( Für weiterführende Studien gibt es ja das Mathe-Lehrbuch ). Wer noch nicht über die grundlegende Bedienung des GTR bescheid weiß, z.Bsp. wie man sich eine Funktion im Graph-Menü in einem geeigneten Fenster anzeigen lässt, der kann das hier erfahren.
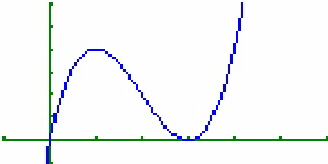
Als Beispielfunktion dient auf dieser Seite die Funktion
f(x)=x³-6x²+9x. Diese Funktion geht durch den Koordinatenursprung ( 0;0 ),
hat ihr Maximum bei ( 1;4 ) und das Minimum bei ( 3;0 ). Das Minimum ist also gleichzeitig
die Nullstelle. Ihren Wendepunkt hat die Funktion bei ( 2;2 ).
Die erste Ableitung : f´(x)=3x²-12x +9
Die zweite Ableitung: f´´(x)=6x-12
Die dritte Ableitung : f´´´(x)=6
5.1 Erläuterung einiger wichtiger Begriffe der Differentialrechnung:
DerDifferentialquotient drückt u. a. den Anstieg der Tangente an einem bestimmten Punkt aus (d.h. den Tangens des Winkels, unter welchem die Tangente an diesem Punkt die x-Achse schneidet). Man bekommt also eine Aussage über das Verhalten der Funktion an dieser Stelle. In der Physik ist der Differentialquotient in einem (s)-(t)-Diagramm zum Beispiel die Momentangeschwindigkeit. Theoretisch wird der Differentialquotient ja so gebildet, dass man durch zwei Punkte einer Funktion eine Sekante legt. Deren Anstieg (=Differenzenquotient) kann man man aus einer 2-Punktegleichung berechnen. Dann läßt man mittels Grenzwertberechnung den Abstand der beiden Punkte gegen Null gehen. Der Differentialquotient ist demzufolge der Grenzwert des Differenzenquotienten.
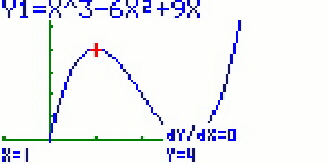
Extrema unterscheiden sich in Maximum und Minimum. Ein lokales Maximum bedeutet, dass alle Funktionswerte in einer bestimmten Umgebung unterhalb der y-Koordinaten des Maximums liegen. Beim Minimum liegen dementsprechend die Funktionswerte in einer bestimmten Umgebung oberhalb der y-Koordinaten des Minimums. Die erste Ableitung der Funktion an der Extremstelle ist stets Null ( f´(x E)=0 ). Die Tangenten an den Extrempunkten sind also waagerecht.
Die erste Ableitung ist an beiden Stellen Null ( dY/dX=0 ).
Legt man an das Maximum eine Tangente an, so kann man gut erkennen, dass diese waagerecht ist.
Damit man den Unterschied besser sieht, wurde die Funktion rot angezeigt. Wie das geht, steht
in der Einführung 1
Wendepunkte sind die Punkte, wo das Schaubild einer Funktion von einer Linkskurve in eine Rechtskurve übergeht bzw. umgekehrt. Eine Linkskurve bedeutet, dass f´(x) mit steigenden x-Werten größer wird (d.h. die Tangenten "hängen" von unten an der Funktion dran). Bei einer Rechtskurve ist es dementsprechend umgekehrt. Mit steigenden x-Werten wird f´(x) kleiner ( die Tangenten "liegen" auf der Funktion ). Und wenn die Funktion von der einen Kurve in die andere übergeht, d.h. die Funktion einen Wendepunkt besitzt, dann ist die zweite Ableitung der Wendestelle stets Null (f´´(xw)=0) und die dritte Ableitung ungleich Null (f´´´(x)<>0). Die Tangenten an den Wendepunktennennt man Wendetangenten. 5.2 Differentialrechnung im Graph-Menü
Wichtig!!:
Die nachfolgenden Anleitungen gehen davon aus, dass die entsprechende Funktion in einem geeigneten Fenster gezeichnet ist. Die Beispielfunktion wird in folgenden Einstellungen angezeigt:
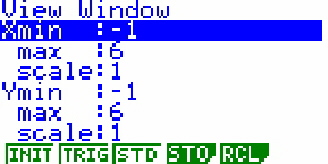
Der Ausgangsbildschirm sieht dann so aus:
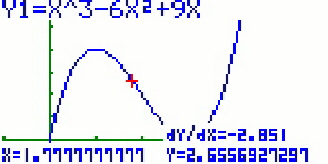
Anzeigen des Differentialquotienten mit Trace
Man kann sich den Differentialquotientenfür einen bestimmten
Punkt einer Funktion anzeigen lassen, während man mit den Cursor-links bzw. Cursor-rechts
Tasten  die Funktion mit dem Cursor sozusagen "abfährt". Mit
die Funktion mit dem Cursor sozusagen "abfährt". Mit
![]() sieht man folgendes Bild:
sieht man folgendes Bild:
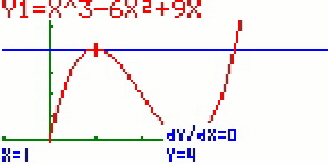
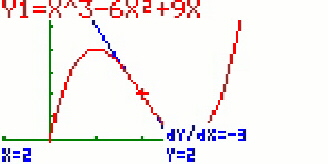
Wer will, kann sich auch eine Tangente oder eine Normale an einem
Punkt anzeigen lassen. Dazu
![]() ,
,
![]() ,
,
![]() (Tang) für die Tangente drücken. Dann den entsprechenden Punkt auswählen und
mit
(Tang) für die Tangente drücken. Dann den entsprechenden Punkt auswählen und
mit ![]() bestätigen. Hier im Bild ist dies die Wendetangente durch den Wendepunkt ( 2;2 ).
bestätigen. Hier im Bild ist dies die Wendetangente durch den Wendepunkt ( 2;2 ).
Möchte man die Normale sehen, geschieht dies durch
![]()
![]()
![]() (Norm). Den Punkt wieder
mit
(Norm). Den Punkt wieder
mit ![]() bestätigen. Der Anstieg
der Normalen beträgt immer -1/m (m ist der Anstieg der Tangenten).
D.h. Tangente und Normale schneiden sich unter 90°.
bestätigen. Der Anstieg
der Normalen beträgt immer -1/m (m ist der Anstieg der Tangenten).
D.h. Tangente und Normale schneiden sich unter 90°.
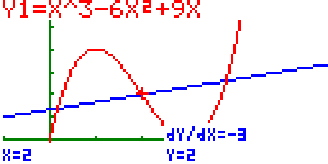
Auch hier gilt, dass man keinen exakten Punkt angeben kann. Will man die Tangente an einem ganz bestimmten Punkt sehen, so muss man sich die Tangentengleichung ausrechnen und als weitere Funktion im Graph-Menü anzeigen lassen.
Ermitteln der ExtrempunkteUm das Maximum bzw. das Minimum einer Funktion zu bestimmen,
ist das Graph-Menü gut geeignet. Es empfiehlt sich, wenn man sich erst die Funktion
mit größeren Fenstereinstellung ansieht und danach das Fenster für die in
Frage kommende Stelle ausrichtet. Mit
![]() und
und
![]() (MAX) wird dann das
Maximum bestimmt, mit
(MAX) wird dann das
Maximum bestimmt, mit
![]() und
und
![]() (MIN) das Minimum.
(DerTaschenrechner benötigt eine kleine Rechenpause.)
(MIN) das Minimum.
(DerTaschenrechner benötigt eine kleine Rechenpause.)
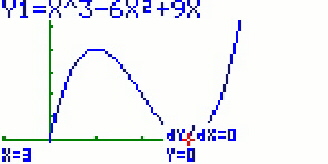
Man bekommt so das Maximum angezeigt:
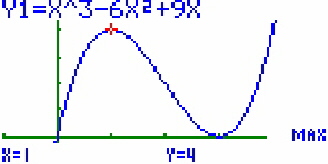
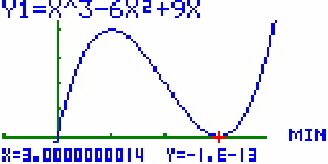
Die entsprechenden x- bzw. y-Werte sind unten eingeblendet.
Hier kann man auch gut die Grenzen des GTR erkennen. Denn bei Lösungen im Graph-Menü
kommt es je nach Einstellung des Fensters zu Rundungsfehlern. Das Minimum liegt
bei M ( 3;0 ), die Anzeige gibt einen geringfügig anderen Wert aus.
Relativ schnell kann man im Run-Menü den
Differentialquotienten berechnen. Dazu muss man sich natürlich im Run-Menü befinden.
Mit ![]() -
- ![]() (CALC)
-
(CALC)
- ![]() (d/dx) sieht man
folgende Anzeige: d/dx( . Nach der Klammer muss jetzt die Funktion eingegeben werden.
Danach ein
(d/dx) sieht man
folgende Anzeige: d/dx( . Nach der Klammer muss jetzt die Funktion eingegeben werden.
Danach ein ![]() und
der x-Wert, für den man den Differentialquotienten wissen möchte.
Für die Beispielfunktion sieht das für den x-Wert =1 so aus:
und
der x-Wert, für den man den Differentialquotienten wissen möchte.
Für die Beispielfunktion sieht das für den x-Wert =1 so aus:
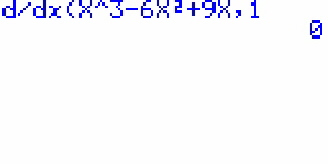
Da die Funktion bei x=1 ihr Maximum besitzt, muß der
Differentialquotient ja Null sein. Hat man die Funktion vorher schon einmal im Graph-Menü
eingegeben, so muß man sie hier im Run-Menü nicht nochmal eingeben. Mit
![]() -
-![]() (GRPH)
-
(GRPH)
-![]() (Y) übernimmt man
Funktionen aus dem Graph- bzw. dem Table-Menü. Nach dem Y muß man die Zeile angeben,
unter der die Funktion gespeichert ist. Ist sie z.B. unter Y1 gespeichert (also als erste
in dieser Form), so braucht man nur die
(Y) übernimmt man
Funktionen aus dem Graph- bzw. dem Table-Menü. Nach dem Y muß man die Zeile angeben,
unter der die Funktion gespeichert ist. Ist sie z.B. unter Y1 gespeichert (also als erste
in dieser Form), so braucht man nur die
![]() drücken und die
Angabe der x-Stelle ist wie oben. Ist die Funktion also im Graph-Menü so gespeichert
:
drücken und die
Angabe der x-Stelle ist wie oben. Ist die Funktion also im Graph-Menü so gespeichert
:
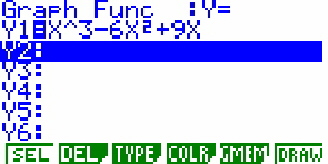

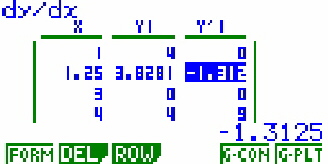
Das heißt, die Funktion hat in dem Punkt
P( 1.25;3,83 ) einen Differentialquotienten von -1,3125.